De la Tetraktys au quatre de chiffre (7)

Nous avons vu qu'en croisant une roue formée des 4 premiers nombres, les nombres de la Tetraktys pythagoricienne, nous obtenons une figure dont les nombres face à face (en suivant les lignes passant par le centre) totalisent 5.
1 + 4 = 5
2 + 3  = 5
5 est le centre invisible de cette figure.

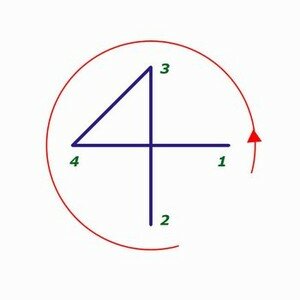
Donc àpartir de la dernière figure de notre précédent message, nous pouvons construire 2 autres figures, une dextrogyre et une senestrogyre :

la première qui donne la progression 1 - 2 - 4 - 3 (en suivant la flèche)

Hors 1 2 4 3 est en rapport avec la série des doubles : 1 2 4 8 

1
2
4
3 => 8 Rajoutons à chaque fois le centre invisible de la croix 5 : 3 + (5 x 1) = 8

et ainsi de suite
1 => 16 = 1 + 5 + 5 = 5  (soit 1 + (5 x 3))
2 => 32 = 2 + 5 + 5 + 5  +  5 + 5 + 5  (soit 2 + (5 x 6))
4 => 64 = 4 + 5 + 5 + 5  +  5 + 5 + 5    +   5 + 5 + 5  +  5 + 5 + 5  (soit 4 + (5 x 12))
3 => 128 = 3 + (5 x 24)

En résumé nous pouvons dire, que les doubles qui dépassent 4 (le dernier nombre des quatre chiffres de la tetraktys) doivent être réduits en soustrayant un multiple de 5 à ce double.
( Multiples de 5 de la série=> 5 x 1, 5 x 3, 5 x 6, 5 x 12, 5 x 24, etc...)
les nombres ainsi obtenus suivent exactement la série à 4 termes :  1 2 4 3 et ceci à l'infini :
1 2 4 3 (1er tour) 1 2 4 3 (2eme tour) etc...

---

et une autre figure dans l'autre sens qui donne la progression 1 - 3 - 4 - 2 (en suivant la flèche)

Nous allons reconnaitre de la même manière dans la série 1 3 4 2 la série des triples 1 3 9 27

1 => 1
3 => 3
4 => 9 = 4 + (5 x 1)
2 => 27 = 2 + (5 x 5)

1 => 81 = 1 + (5 x16)
3 => 243 = 3 + (5 x 48)
4 => 729 = 4 + (5 x 145)
2 => 2187 = 2 + (5 x 437)