Je terminais mon post du 31 décembre 2010 par cette série découlant des réductions des tiers (1/3) moins l'unité des puissances de 7 :
2, 7, 6, 8, 4, 3, 5, 1

On tombe sur la série (dans l'ordre inverse) des réductions des nombres pentagonaux n (3n - 1) / 2 :
1, 5, 3, 4, 8, 6, 7, 2

En effet :

 1   >  1
 5   >  5
12  >  3
22  >  4
35  >  8
51  >  6
70  >  7
92  >  2

Voici un petit jeu numérique qui m’avait fait penser au problème des 7 maisons du papyrus Rhind :

Le problème 79 porte sur un domaine composé de 7 maisons dans lesquelles il y
a 7 chats qui mange 7 souris qui avaient mangé 7 semences qui pouvaient rapporter
7 hekats de grain. La question est de savoir combien de hekats de blé ont été perdus.

Ce problème selon le scribe viendrait d’une source plus ancienne remontant aux Babyloniens

maisons 7   (7)
chats 49  (7x7)
souris 343  (7x7x7)
semences 2 401 (7x7x7x7)
hekats 16 807 (7x7x7x7x7)

Le résultat s’arrête à la puissance 5 de 7
Dans le papyrus qui est parvenu jusqu’à nous, la 4ème puissance donne 2301 à la place de 2401 bien que le résultat final de 16807 soit juste…
Je me suis demandé si le scribe n’avait pas voulu attirer volontairement notre attention sur une erreur qui aurait pu cacher autre chose…

Mais je n’ai rien trouvé de ce genre  …  Peut être autre chose, les puissances de 7 sont toutefois très intéressantes à étudier. Je vais vous faire part de ces observations.

Mon axiome : Toutes les puissances de 7 sont composées de trois parties égales auxquelles on y ajoute l’unité.

Exemple pour la première. (2 + 2 + 2) + 1 = 7
pour la seconde (16 + 16 + 16) + 1 = 49
Etc…

Disposons les nombres des puissances de 7 auxquelles nous aurons enlevé l’unité et  prenons le tiers, le tiers multiplié par 2 et la totalité des 3 tiers.

Plaçons en face la réduction dite théosophique.

2  2
4  4
6 6

16  7
32  5
48  3

114  6
228  3
342  9

800  8
1600  7
2400 6

5602  4
11204  8
16806  3

39216  3
78432  6
117648 9

274514 5
549028 1
823542 6

1921600 1
3843200 2
5764800 3

13451202 9
26902404 9
40353606 9

Nous sommes arrivés à la 9ème puissance de 7,  Il semblerait qu’un mécanisme régisse ces puissances à l’infini par groupe de 9.

Prenons la série obtenue avec les tiers :
2, 7, 6, 8, 4, 3, 5, 1, 9
Un polygramme pourrait être dessiné avec cette séquence.

Ca faisait un moment que je m'intéressais au symbolisme de la marelle.
J'ai trouvé à son sujet des choses intéressantes sur le net, des études, conférences, etc...
Mais rien concernant la disposition des notes de musique sur les cases de ce jeu.
En effet, la marelle est composé de 8 cases entre Terre et Ciel, et cela me faisait penser donc à une octave complète par exemple de Do à Do il y a huit notes (octave)

Voici un dessin de marelle :

On pélegrine à cloche pied entre les huit cases en poussant un galet, d'abord 1 puis 2 , 3, etc... et chaque fois on rrevient en ramassant le galet. On ne peut poser les deux pieds seulement sur les cases  4 - 5 et  7 - 8
J'ai donc pensé à placer les "accidents" de la gamme à ces endroits particuliers (les fameux demi-tons)

Voir les dessins ci-dessous :

Qu'en pensez-vous? voyez-vous d'autres dispositions afin de faire figurer les demi-tons de la gamme? en accord avec le dessin du jeu de la marelle?

Je voudrais commencer une étude sur le nombre 17 en publiant ici une partie d'un message que j'ai envoyé à un ami.
Le nombre 17 a fait couler beaucoup d'encre dernièrement, notamment par les chercheurs qui ont parlé de Rennes le Château ou du Prieuré de Sion.

A ma manière et selon ma formation, je voudrais ici exposer certaines particularités mathématiques de ce nombre.

Le nombre 17 quand on le divise propose de curieuses décimales :

1/17 :              0,0588235294117647 0588235294117647 ................

2/17 :             0,1176470588235294 1176470588235294

3/17 :              0,1764705882352941 1764705882352941

4/17 :              0,2352941176470588 2352941176470588

5/17 :              0,2941176470588235 2941176470588235

6/17 :              0,3529411764705882 3529411764705882

7/17 :              0,4117647058823529 4117647058823529

8/17 :              0,4705882352941176 4705882352941176

9/17 :              0,5294117647058823 5294117647058824

10/17 :            0,5882352941176470 5882352941176471

11/17 :            0,6470588235294117 6470588235294118

12/17 :            0,7058823529411764 7058823529411765

13/17 :            0,7647058823529411 7647058823529412

14/17 :            0,8235294117647058 8235294117647059

15/17 :            0,8823529411764705 8823529411764706

16/17 :            0,9411764705882352 9411764705882353

Ces décimales se répètent à l’infini par groupes de 16 nombres…. Ce sont toujours les mêmes nombres qui les composent dans le même ordre

Dans un groupe par ex : 0588235294117647 il y a une symétrie par rapport à 9

05882352

94117647

Prenons 0 +9 = 9, 5+4, 8+1, 8+1, 2+7, 3 + 6, 5+4, 2+7, etc….

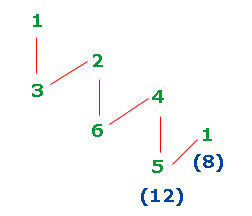
On pourra comprendre que l’on peut tracer une rosace étoilée à 16 points (formée de 2 roues  à 8 points de centre 9…)

Dans un premier temps par exemple, cela me fait penser à l'étoile à 16 branche de Baux en Provence

Voici  un procédé très simple attribué à Nicomaque pour trouver les nombres de l'âme du Monde.

Il faut disposer sur les branches d'un triangle d'un côté la série des doubles et de l'autre la série des triples.
(nombres en gras)

Pour remplir le tableau, il faut additionner chaque nombre pris deux par deux de la ligne supérieure et ensuite inscrire le résultat sur la ligne d'en dessous.

Soustrayons à chaque nombre de ce tableau le  nombre  7 ou les multiples de 7 approchant ce nombre pour voir apparaître la séquence :

132645

Examinons notre table H en donnant la réduction dite somme théosophique.
Nous pouvons voir dans cette table 2 séries 124875 (voir le monogramme AM)

Comparaison avec la table H et la série 132645 :

Nous pouvons voir se dérouler 4 séries 132645

Je pense que certains lecteurs de ce blog n’auront pas manqué de faire le lien entre nos derniers messages et les fameux calculs de l’âme du monde.
En effet il s’agit bien de cela.  M. G. était sans doute un très grand initié, il a su avec le langage de son époque offrir de nouvelles pistes afin de faciliter la compréhension de cette connaissance voilée ainsi qu’un excellent symbole inconnu, synthése de cette connaissance et qui est une sorte d’ordinateur.
J'ai essayé selon mes connaissances de vous presenter les rudiments de "la mécanique" de ces figures qui font appel aux croisements : d'abord les carrés torsadés au centre 5 donnant la série des doubles dans un sens (1243) et la série des triples (1342) dans l'autre sens.

http://zanoni.canalblog.com/archives/p13-3.html

http://zanoni.canalblog.com/archives/2007/06/20/5368394.html

Ensuite, les figures aux croisements plus complexes, celles qui donnent la séquence 132645 et le Monogramme de Marie en rapport avec la séquence 124875 et la série des doubles à 6 termes qui se répète à l'infini ( 1 : 2; 4; 4; 8; 7 (16 => 1 +6 = 7) ; 5 (32 => 3 + 2 = 5) ensuite on recommence à 1 qui est 64 (6 + 4 = 10 => 1 + 0 = 1)

Les réductions comme les additions dites théosophiques étaient connues depuis longtemps, elles ne servaient pas qu'à la numérologie, mais elles faisaient partie d'une science arithmétique inconnue.

Nous verrons par exemple par la suite, que le procédé de Nicomaque obéit également à la séquence 132645, je ne sais pas si cette séquence était connue de Nicomaque mais elle synthétise arithmétiquement les calculs de l’âme du monde.

Pour le moment, voici une figure à titre de curiosité, qui montre que Robert Fludd s’intéressait également à la représentation de l’âme du monde.

cette mécanique de la loi de trois et suivant la séquence 132645 explique la permutation que l'on trouve dans la table des hydrogènes de M. G.

Voilà pourquoi 1 ; 2 ; 3 devient 1 ; 3 ; 2 et ceci à l'infini, comme nous l'avons vu dans le message précédent, du moins jusqu'à 6144 de la table ci-dessous.

Mes derniers messages portent sur la table des hydrogènes de M. G. qui figure dans les « Fragments d’un enseignement inconnu » d’Ouspensky ou  « In Search of the Miraculous » le même livre en anglais.

Pour ceux qui désirent le télécharger voici la version anglaise :

http://zone-7.net/bibliotheque/index.php?path=---+Section+Anglaise+---%2FTraditional+teachings/

Voici ci-dessous une figure de la table des hydrogènes tirée de ce livre :

« Sources de divines
Joies, révolte et souffrances,
Dirigez votre action sur nous. »

Revenons à notre séquence 1 3 2 6 4 5
Beaucoup ont parlé de la loi de trois mais peu l’ont fait en rapport avec 1 3 2 6 4 5.
Je vais tacher de donner quelques explications.

Reprenons un extrait  des Récits de Belzébuth à son petit fils de M. G., chapitre la sainte planète du purgatoire p222 de mon édition (Rocher/Littéraure) :
« Tout nouveau surgissement provient de surgissements antérieurs par le « harnel-miatznel », c'est-à-dire par une fusion dont le processus s’accomplit ainsi ; ce qui est en haut s’unit à ce qui est en bas, afin de réaliser par cette union  ce qui est médian, lequel devient alors à la fois le supérieur pour l’inférieur suivant, et l’inférieur pour le supérieur précédent. »

1 s’unit à l’inférieure 3, cette union donne 2 qui est la moyenne arithmétique (1+3)/2 = 2, 2 est le supérieur suivant, il s’unit avec l’inférieur 6 suivant, cette union donne 4 (4 = (2+6)/2), 4 est le supérieur suivant il s’unit avec 12 qui est représenté dans cette séquence par 5 (7x1 + 5 = 12) ; cette union donne 8 (8= (4 + 12)/2)  qui est representé par 1 (7x1 + 1 = 8) ; etc… et ceci mathématiquement à l'infini

Nous avons vu que dans le cas de notre polygramme
http://zanoni.canalblog.com/archives/2007/07/26/5723651.html#comments

Il faut ajouter 7 qui est le centre de la figure pour obtenir les progressions géométriques enchevétrées de la séquence, et cela à l’infini :
1 ; 2 ; 4 ; 1  (7x1 + 1 = 8) ; 2  (7x2 +2 = 16) ;   (7x4 + 4 = 32)  etc…
Et
3 ; 6 ; 5 (7x1 + 5 = 12) ; 3 (7x3 + 3 = 24) ; 6 (7x6 + 6 = 48)

En fait :
1 ; 2 ; 4 ; 8 ; 16 ; 32 ; etc…
Et
3 ; 6 ; 12 ; 24 ; 48 : etc…

http://zanoni.canalblog.com/archives/2007/07/27/5736790.html#comments